Neural Geometry Fields for Meshes
TL;DR
A neural representation for triangle meshes that encodes geometry as a coarse set of quadrangular patches together with coordinate networks that displace each patch to recover fine detail. Standard meshes are obtained by sampling the displacement field, and the representation yields substantial reductions in mesh memory footprint.
Abstract
Recent work on using neural fields to represent surfaces has resulted in significant improvements in representational capability and computational efficiency. However, to our knowledge, most existing work has focused on implicit representations such as signed distance fields or volumes, and little work has explored their application to discrete surface geometry, i.e., 3D meshes, limiting the applicability of neural surface representations.
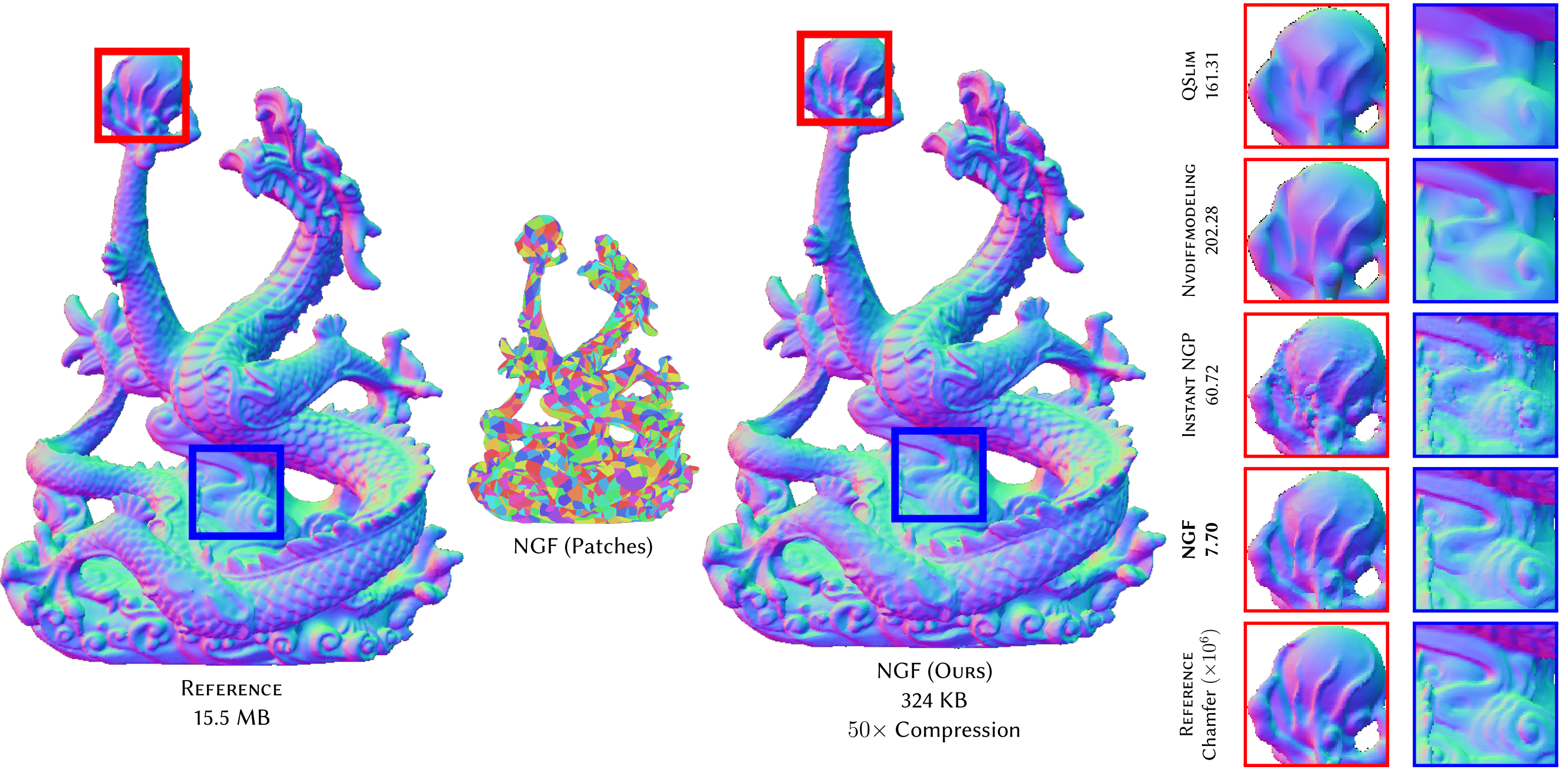
We present Neural Geometry Fields, a neural representation for discrete surface geometry represented by triangle meshes. Our idea is to represent the target surface using a coarse set of quadrangular patches, and add surface details using coordinate neural networks by displacing the patches. We then extract a traditional triangular mesh from a neural geometry field instance by sampling the displacement. We show that our representation excels in mesh compression, where it significantly reduces the memory footprint of meshes without compromising on surface details.